Quiz
Standing waves are produced by the superposition of two waves with
a. the same amplitude, frequency, and direction of propagation.
b. the same amplitude and frequency, and opposite propagation directions.
c. the same amplitude and direction of propagation, but different frequencies.
d. the same amplitude, different frequencies, and opposite directions of propagation.
Answer) b.
Standing wave patterns are produced as the result of the repeated interference of two waves of identical frequency while moving in opposite directions along the same medium.
Standing Waves Simulation
When the next simulation is not visible, please refer to the following link.
(https://helpx.adobe.com/flash-player/kb/enabling-flash-player-chrome.html)
Standing Waves
When two waves move in opposite directions, through each other, interference takes place. If the two waves have the same frequency and wavelength then a specific type of constructive interference can occur: standing waves can form.
Standing waves are disturbances which don't appear to move, they look like they stay in the same place even though the waves that from them are moving. Lets demonstrate exactly how this comes about. Imagine a long string with waves being sent down it from either end. The waves from both ends have the same amplitude, wavelength and frequency as you can see in the picture below:
To stop from getting confused between the two waves we'll draw the wave from the left with a dashed line and the one from the right with a solid line. As the waves move closer together when they touch both waves have an amplitude of zero:
If we wait for a short time the ends of the two waves move past each other and the waves overlap. Now we know what happens when two waves overlap, we add them together to get the resulting wave.
Now we know what happens when two waves overlap, we add them together to get the resulting wave. In this picture we show the two waves as dotted lines and the sum of the two in the overlap region is shown as a solid line:
The important thing to note in this case is that there are some points where the two waves always destructively interfere to zero. If we let the two waves move a little further we get the picture below:
Again we have to add the two waves together in the overlap region to see what the sum of the waves looks like.
In this case the two waves have moved half a cycle past each other but because they are out of phase they cancel out completely. The point at 0 will always be zero as the two waves move past each other.
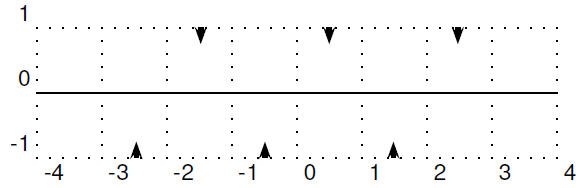
When the waves have moved past each other so that they are overlapping for a large region the situation looks like a wave oscillating in place. If we focus on the range -4, 4 once the waves have moved over the whole region. To make it clearer the arrows at the top of the picture show peaks where maximum positive constructive interference is taking place. The arrows at the bottom of the picture show places where maximum negative interference is taking place.
As time goes by the peaks become smaller and the troughs become shallower but they do not move.
For an instant the entire region will look completely flat.
The various points continue their motion in the same manner.
Eventually the picture looks like the complete reflection through the x-axis of what we started with:
Then all the points begin to move back. Each point on the line is oscillating up and down with a different amplitude.
If we superimpose the two cases where the peaks were at a maximum and the case where the same waves were at a minimum we can see the lines that the points oscillate between. We call this the envelope of the standing wave as it contains all the oscillations of the individual points.
A node is a place where the two waves cancel out completely as two waves destructively interfere in the same place. An anti-node is a place where the two waves constructively interfere.
Important: The distance between two anti-nodes is only 1/2$\lambda$ because it is the distance from a peak to a trough in one of the waves forming the standing wave. It is the same as the distance between two adjacent nodes. This will be important when we workout the allowed wavelengths in tubes later. We can take this further because half-way between any two anti-nodes is a node.
Then the distance from the node to the anti-node is half the distance between two anti-nodes. This is half of half a wavelength which is one quarter of a wavelength, 1/4$\lambda$
To make the concept of the envelope clearer let us draw arrows describing the motion of points along the line.
Every point in the medium containing a standing wave oscillates up and down and the
amplitude of the oscillations depends on the location of the point. It is convenient to draw the envelope for the oscillations to describe the motion. We cannot draw the up and down arrows for every single point!